Modulstruktur
Wir haben gesehen, dass einzelne Module einer Software miteinander interagieren, um die Funktionalität erfüllen zu können. Ein Modul steht also immer mit einem oder mehreren anderen Modulen in Beziehung. In diesem Artikel schauen wir uns an, wie wir diese Beziehungen formalisieren können.
Modulbeziehung als Zweistellige (binäre) Relation
Wir betrachten im Folgenden eine Menge von Modulen \(S = \{ M_1, \ldots, M_n \}\). Was genau diese Module sind, ist für uns im Moment nicht wichtig. Es geht nur um deren Beziehung. Falls Sie sich aber etwas konkretes darunter vorstellen wollen, denken Sie an Klassen in Java.
Um die Beziehung zwischen Modulen auszudrücken, verwenden wir eine zweistellige (oder binäre) Relation. Eine binäre Relation \(r\) ist definiert als eine Teilmenge \(r \subset S \times S\) aller Paare von Modulen. Wir schreiben \(M_i\, r\, M_j \text{ falls } (M_i, M_j) \in r,\) und meinen damit, dass das Module \(M_i\) in Beziehung (gemäss Relation \(r\)) mit \(M_j\) steht.
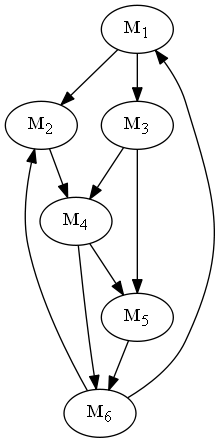
Als Beispiel nehmen wir die Menge \(S = \{M_1, \ldots, M_6\}\). Es gilt also, dass \(r \subset \{(M_1, M_1), (M_1, M_2), \ldots, (M_6, M_5), (M_6, M_6) \}\). Beispielsweise können wir die Relation \(r = \{ (M_1, M_2), (M_1, M_3), (M_2, M_4), (M_3, M_4), (M_3, M_5), (M_4, M_5), (M_4, M_6), (M_5, M_6), (M_6, M_2), (M_6, M_1) \}\) definieren. Binäre Relationen lassen sich als gerichtete Graphen darstellen. Für die oben definierte Relation \(r\) sieht der Graph wie folgt aus.
Transitive Hülle
In der Graphendarstellung sehen wir bereits, dass gemäss Relation \(r\), \(M_1\) und \(M_4\) nicht direkt in Relation stehen, jedoch indirekt miteinander verbunden sind. Um dieses intuitive Konzept zu formalisieren, führen wir die Transitive Hülle ein. Die Transitive Hülle ist definiert als
\[\begin{align} &M_i\, r^+\, M_j \text{ genau dann, wenn } \\ &M_i\, r \, M_j \\ &\text{ oder } \\ &\exists M_k \in S \; \text{so dass} \; M_i r M_k \text{ und } M_k r^+ M_j \end{align}.\]Wir können uns das so merken, dass ein Module \(M_j\) genau dann in der Transitiven Hülle von \(M_i\) ist, wenn es einen (gerichteten) Pfad zwischen den zwei Modulen im Graphen gibt.
Hierarchien und Ebenen
Wie wir später sehen werden, gibt es gewisse Anordnungen von Modulen, die spezielle geeignet sind für Software Engineering. Eine besonders vorteilhafte Anordnung ist die Hierarchie. Hierarchien sind Anordnungen, bei der wir jedem Modul eindeutig einer Ebene zuordnen können. Wir definieren nun die Begriffe Hierarchie und Ebene formal.
Eine binäre Relation \(r\) ist eine Hierarchie genau dann, wenn
\(\nexists (M_i, M_j) \text{ so dass } M_i \, r^+ \, M_j \text{ und } M_j \, r^+ \, M_i\) Diese Definition sagt nichts anderes, als dass es keine Zyklen im Graphen gibt.
Wir können uns die Ebene eines Moduls in der Relation wie folgt definieren:
- \(M_i\) ist auf Ebene 0, falls \(\nexists M_j, \text{ so dass } M_i r M_j\)
- Sei \(k\) die höchste Ebene aller Module \(M_j\), so dass \(M_i r M_j\). Dann ist \(M_i\) auf Ebene \(k+1\)
Übung:
Schauen Sie sich folgenden Graph an und beantworten Sie die folgenden Fragen:

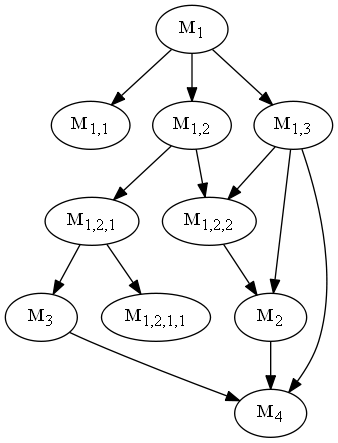
- Welcher dieser Graphen beschreibt eine Hierarchie?
- Was ist die transitive Hülle von \(M_2\) im zweiten Graphen
- Auf welcher Ebene ist Knoten \(M_{1,3}\) im zweiten Graphen?
Notieren Sie sich ihre Antworten, da Sie diese für den Adam Test noch brauchen werden.