Binäre Suchbäume

Im letzten Lernmodul haben wir uns Symboltabellen angeschaut und eine erste, einfache Implementation dieses Datentyps gesehen.

Zur Erinnerung wiederholen wir hier nochmals die Definition vom Datentyp Symboltabelle. Wir haben uns Symboltabellen wie folgt definiert:

class ST[Key, Value]:
    def put(key : Key, value : Value) -> None
    def get(key : Key) -> Value
    def contains(key : Key) -> Boolean
    def delete(key : Key) -> None
      def isEmpty() -> Boolean
    def size() -> Int
    def keys() : Iterator[Key]

Die beiden wichtigsten Operationen sind put um einen Wert unter einem gegebenen Schlüssel in der Symboltabelle zu speichern und get um den Wert wieder zu lesen.

Unsere erste Implementation hat als Datenstruktur ein geordnetes Array verwendet. Die Methode put hat dann jedes Element an der richtigen Stelle im Array hinzugefügt. Wir haben die Ordnung der Elemente im Array ausgenutzt, um mit Hilfe einer binären Suche den Schlüssel, respektive die Stelle in der wir einen neuen Schlüssel einfügen müssen, effizient zu finden. Binäre Suche findet das richtige Element respektive die richtige Stelle zum Einfügen eines Elements im schlechtesten Fall in \(O(\log_2(N))\) Schritten. Das bedeutet, dass wir sehr effizient Suchen können. Obwohl wir auch beim Einfügen die richtige Stelle zum Einfügen schnell finden, können wir das Element nicht effizient einfügen, da wir alle nachfolgenden Elemente um eine Position nach hinten schieben müssen. Ein Array ist also offensichtlich nicht die ideale Datenstruktur um Symboltabellen zu implementieren. Wir schauen uns deshalb nun eine zweite Implementation an, bei der wir binäre Suchbäume verwenden. Obwohl binäre Suchbäume im schlechtmöglichsten Fall lineare Komplexität sowohl für das Auffinden eines Schlüssels als auch für das Einfügen haben, können beide Operationen im Durchschnitt in logarithmischer Zeit durchgeführt werden. Durch die Verwendung von verketteten Knoten für die Repräsentation von Bäumen, können wir im Gegensatz zu Arrays an jeder Stelle effizient neue Knoten hinzufügen.

Datenstruktur

Ein binärer Suchbaum ist ein Binärbaum mit symmetrischer Ordnung. Wir wissen bereits was ein Binärbaum ist, nämlich ein Baum, in dem jeder Knoten maximal zwei Unterbäume (Kinder) hat. Symmetrische Ordnung ist wie folgt definiert:

Ein Baum hat symmetrische Ordnung, wenn der Schlüssel jedes Knotens

• grösser ist als alle Schlüssel im linken Teilbaum
• kleiner ist als alle Schlüssel im rechten Teilbaum.

(Da Schlüssel in der Symboltabelle eindeutig sein müssen, können keine zwei Schlüssel gleich sein)

Die folgende Abbildung zeigt den Schematischen Aufbau eines binären Suchbaums sowie ein Beispiel eines Suchbaums. Der Beispielbaum zeigt den binären Suchbau, den wir erhalten wenn wir die Schlüssel S E A R C H E X A M P L E in dieser Reihenfolge in den Baum einfügen. Der zum Schlüssel entsprechende Wert ist die Position des Buchstabens im String SEARCHEXAMPLE.

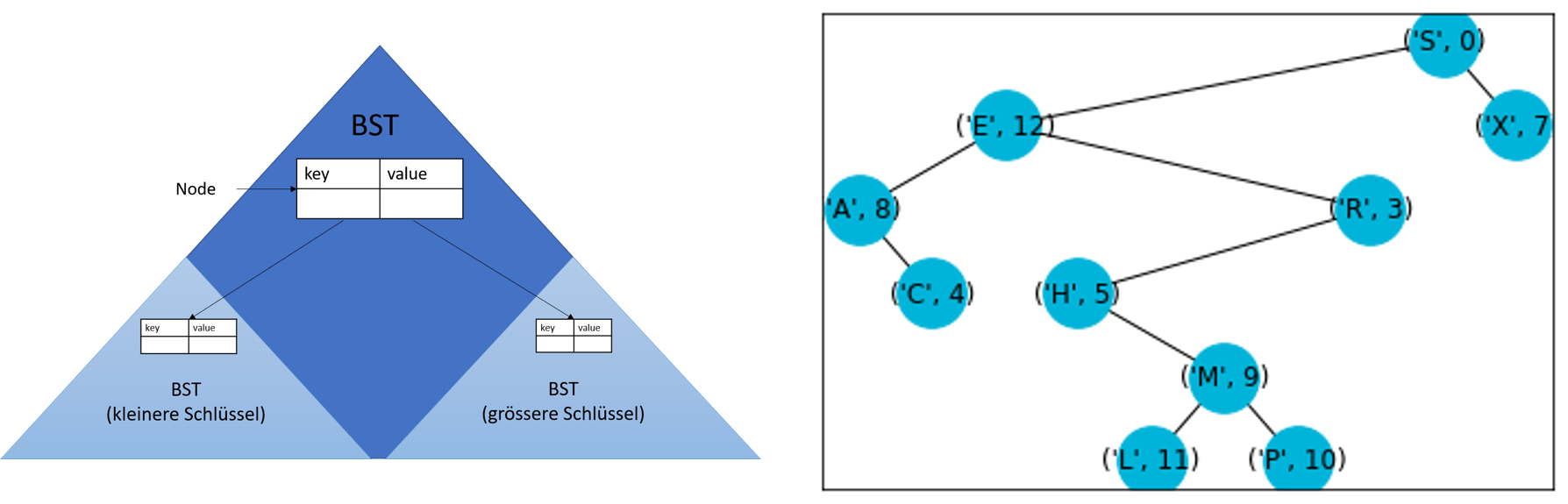
Suchen, Einfügen und Löschen

Wie wir im folgenden Video sehen werden, können wir die Operationen get und put mit sehr wenig Code implementieren. Die Implementation der put Operation ist aber etwas trickreich. Auch die Operation delete ist nicht ganz trivial. In allen Fällen können wir die Implementation aber gut verstehen, indem wir uns die entsprechende Datenstruktur grafisch aufzeichnen und uns die einzelnen Schritte an konkreten Beispielen überlegen.

Nachdem Sie sich das Video angeschaut haben, sollten Sie deshalb unbedingt auch mit dem entsprechenden Jupyter Notebook arbeiten.

• Slides (pdf)

• Jupyter-Notebook (Vorschau)
• Jupyter-Notebook (Download) (Speichern mit Rechtsklick, Speichern unter)

Eigenschaften und Komplexität

Aus unseren Experimenten im vorigen Jupyter-Notebook wird unmittelbar klar, dass die Zeit die benötigt wird um einen neues Schlüssel-Werte Paar einzufügen, oder um einen bestehenden Schlüssel zu suchen, von der Ausprägung des Baumes abhängt. Die nachfolgende Abbildung zeigt zwei extreme Ausprägungen von binären Suchbäumen. Der Baum links ist der perfekte Baum und der Baum rechts entspricht einer Liste. Wenn wir in unserem Beispiel den Schlüssel J in den Baum einfügen, benötigen wir im Baum links nur 3 Vergleiche, während wir im Baum rechts 7 Vergleiche brauchen. Allgemeiner, brauchen wir für das Einfügen eines Schlüssels in den perfekten Binärbaum \(O(\log_2(N))\) Operationen und für das Einfügen in die Liste \(O(N)\) Operationen, wobei N die Anzahl Knoten bezeichnet.

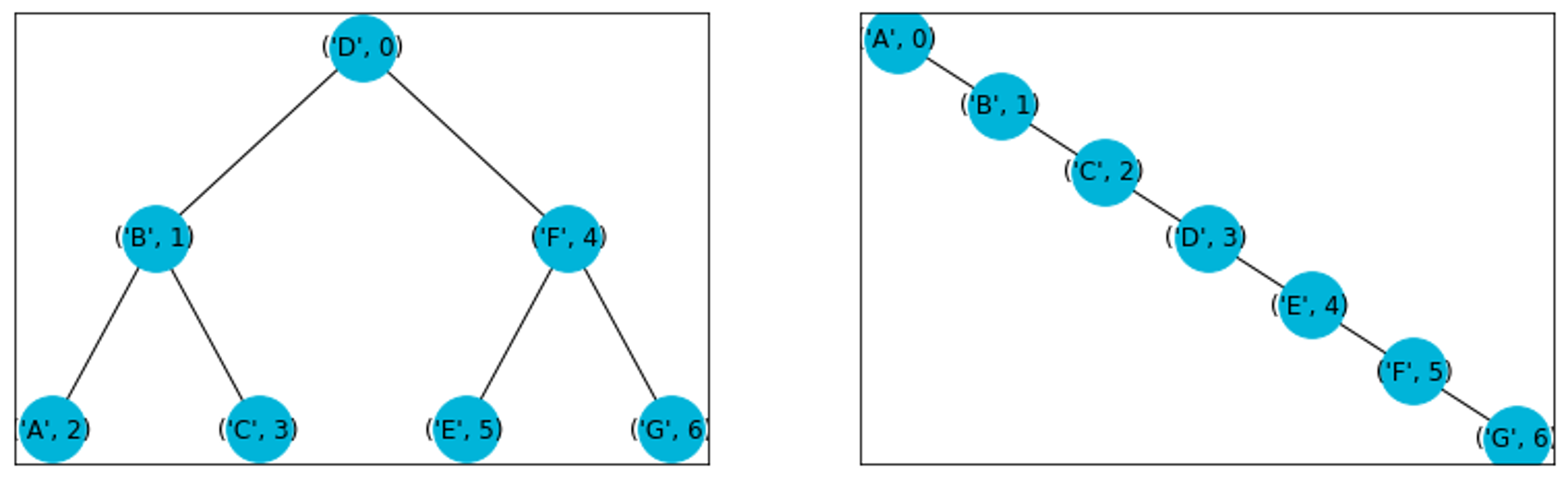
In der Praxis wird die Ausprägung vom Baum irgendwo zwischen den zwei Extremen liegen. Die Extreme sind sehr unwahrscheinlich und entsprechen sehr speziellen und seltenen Konfigurationen. Wenn wir zufällige Sequenzen betrachten, werden diese also im allgemeinen zwar nicht einer perfekten Baumstruktur entsprechen, aber trotzdem eine typische Baumstruktur aufweisen. Man kann zeigen, dass bei \(N\) gleichverteilten Schlüsseln, die durchschnittliche Tiefe eines Knotens ungefähr \(1.39 \log_2(N)\) entspricht. Entsprechend erwarten wir für durchschnittliche Schlüssel, dass wir einen Schlüssel im Schnitt mit \(1.39 \log_2(N)\) Operationen in einem Baum mit \(N\) Knoten finden. Für einen formalen Beweis dieser Tatsache, verweisen wir auf Satz C und D in Abschnitt 3.2 vom Buch Algorithmen, von Robert Sedgewick und Kevin Wayne.

Unsere bisherigen Implementation von Binärsuchbäumen weisen folgende Laufzeitkomplexität auf:

	Durchschnittlicher Aufwand		Schlechtester Fall
	Einfügen	Suchen	Einfügen	Suchen
Binäre Suche	O(N)	O(log(N))	O(N)	O(log (N))
Binäre Suchbäume	O(log(N))	O(log(N))	O(N)	O(N)

Es gibt Erweiterungen vom binären Suchbaum, die sicherstellen, dass der Baum beim Einfügen immer ausgeglichen bleibt. Eine populäre Implementation eines solchen balancierten Suchbaums ist der sogenannte Rot-Schwarz Baum. Beim Rot-Schwarz Baum kann auch im schlechtesten Fall die Laufzeit von \(O(\log(N))\) für Einfügen und Suchen garantiert werden.