Übungsblatt 9: Anwendungen der Graphenexploration

Bei Aufgabe 1 und 2: Wenn Sie Knoten in beliebiger Reihenfolge betrachten können, dann wählen Sie jeweils wieder den Knoten mit dem kleinsten Schlüssel.

Aufgabe 1

Betrachten Sie folgenden gerichteten Graphen:

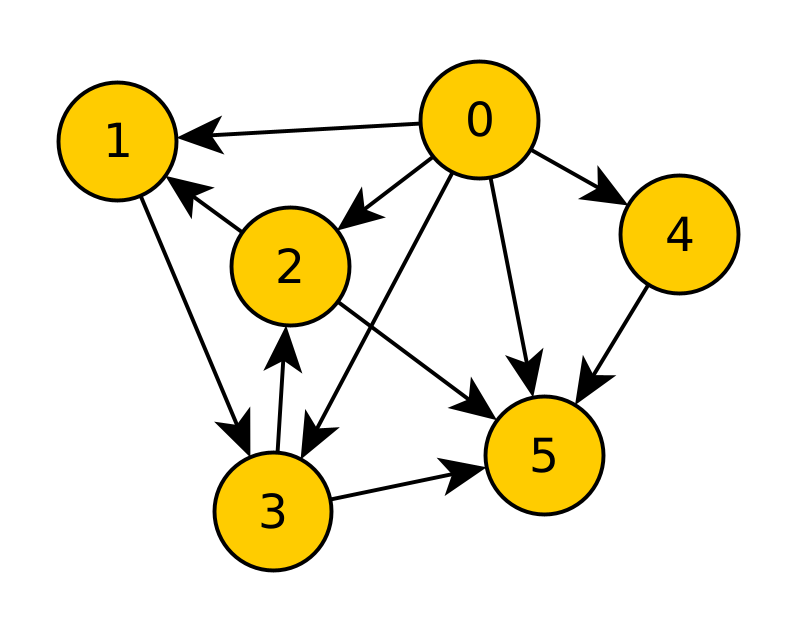
Verwenden Sie das Verfahren aus der Vorlesung, um zu prüfen, ob der Graph azyklisch ist. Finden Sie einen Zyklus? Falls ja, welchen?

Aufgabe 2

Betrachten Sie folgenden gerichteten Graphen:

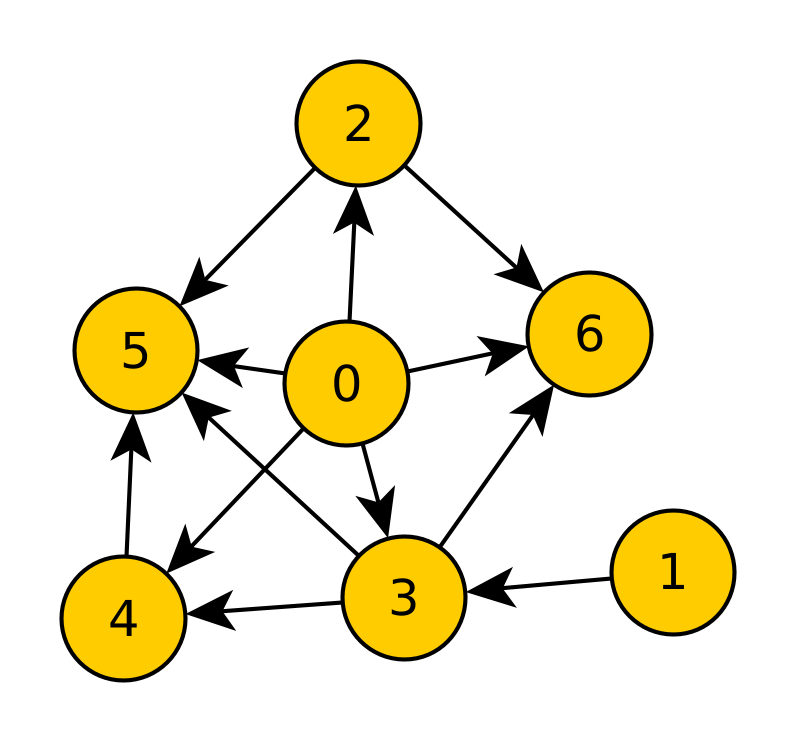
• Ist der Graph azyklisch?
• Geben Sie zwei verschiedene topologische Sortierungen an.
• Spielen Sie von Hand den Algorithmus zum Finden topologischer Sortierungen aus dem jupyter-Notebook nach. Welche Sortierung erhalten Sie?

Aufgabe 3

Für diese Aufgabe haben wir für Sie bereits ein Projekt mit allen benötigten Sourcen, einer Testumgebung sowie einem Buildsystem vorbereitet. Sie können dieses als Zip-Archiv herunterladen

• Zip-Archiv zur Übung

Im Rahmen dieser Aufgabe implementieren Sie den Algoritmus von Kosaraju zum Finden aller starken Zusammenhangskomponenten in einem gerichteten Graphen. Für die Repräsentation der Graphen verwenden wir JGraphT. Sie finden die relevant API hier.

Ihre Implementierung muss nur Graphen vom Typ Graph<Integer, DefaultEdge> unterstützen.

• Implementieren Sie getGraphWithReversedEdges, so dass für Eingabegraphen \(G = (V, E)\) der Graph \(G^R = (V, \{(v,u)\mid (u,v)\in E\})\) erstellt und zurückgegeben wird.

• Implementieren Sie getReversedPostorder, um eine umgekehrte Postorder-Reihenfolge der Knoten in dem Eingabegraphen zu bestimmen. Denken Sie dabei daran, dass alle Knoten des Graphen erfasst sein sollen, nicht nur die von einem Ausgangsknoten erreichbaren Knoten.

  Als Unterfunktion sollten Sie dabei depthFirstExploration für die Tiefensuche verwenden. Implementieren Sie diese ebenfalls im Rahmen dieser Teilaufgabe.

• Jetzt haben Sie alle notwendigen Komponenten für den Algorithmus von Kosaraju implementiert. Vervollständigen Sie nun getStronglyConnectedComponents in geeigneter Weise.

  Hinweis: Die Knoten, die innerhalb eines Aufrufs von depthFirstExploration zur reversedPostOrder hinzugefügt werden, entsprechen bei einer korrekten Implementierung allen vom Startknoten aus erreichbaren Knoten.

Hinweis: Es kann beim Debuggen hilfreich sein, den Graphen auszugeben und anzuzeigen. Mit der Methode toString() erhalten Sie eine String-Repräsentation des Graphen, bestehend aus der Liste der Knoten und der Liste der Kanten. Mit Hilfe von Exercise9.writeGraph können Sie Graphen auch im DOT-Format in eine Datei schreiben und mit einem Anzeigeprogramm Ihrer Wahl (z.B. mit Graphviz) rendern.

Harte Nuss

*Diese Aufgabe ist nur für diejenigen gedacht, die einen Mathematik-Hintergrund haben und eine Herausforderung suchen. Der Schwierigkeitsgrad liegt deutlich über dem, was wir in der Klausur erwarten.

(Es ist aber eine Aufgabe, die die Informatik-Studierenden als Teil des normalen Übungsbetriebs lösen, und die damit für sie auch für die Klausurzulassung relevant ist.)*

Im Rahmen dieser Aufgabe beweisen Sie die Korrektheit des Algorithmus von Kosaraju zum Finden aller starker Zusammenhangskomponeten in einem gerichteten Graphen \(G\).

Wenn Sie eine Teilaufgabe nicht beweisen können, dürfen Sie die entsprechende Aussage dennoch in den folgenden Teilaufgaben verwenden.

1. Zeigen Sie: Gibt es in einem Graphen einen Pfad von Knoten \(u\) zu Knoten \(v\) aber nicht umgekehrt, so kommt Knoten \(u\) in der umgekehrten Postorder-Reihenfolge vor Knoten \(v\). Tipp: Machen Sie eine Fallunterscheidung, ob \(v\) bereits einmal besucht wurde, bevor die Tiefensuche zum ersten Mal für Knoten \(u\) aufgerufen wird.
2. Zeigen Sie: Gibt es in einem Graphen \(G\) einen Pfad von Knoten \(u\) zu Knoten \(v\), aber nicht umgekehrt, so kommt Knoten \(v\) in der umgekehrten Postorder-Reihenfolge für den transponierten Graphen \(G^{\textup{R}}\) vor Knoten \(u\).
   Tipp: Können Sie Ihr vorheriges Ergebnis verwenden?
3. Sei \(R\) die umgekehrte Postorderreihenfolge von Graph \(G^{\textup{R}}\) und sei \(u\) in \(R\) vor \(v\).
   Zeigen Sie: Ist in Graphen \(G\) Knoten \(v\) von \(u\) aus erreichbar, so gibt es in \(G\) auch einen Pfad von \(v\) zu \(u\).
   Tipp: Führen Sie einen Widerspruchsbeweis.

4. Mit Teilaufgabe 3 haben Sie bereits den starken Zusammenhang der in jeder Exploration erfassten Knoten bewiesen. Es fehlt jedoch noch der Beweis, dass diese Mengen maximal gross sind.

   Zeigen Sie: Sind Knoten \(u\) und \(v\) in der gleichen starken Zusammenhangskomponente von Graphen \(G\), so führt der Algorithmus von Kosaraju einen Explorationsschritt durch, der sowohl \(u\) als auch \(v\) erfasst.

Wir werden diese Aufgabe voraussichtlich nicht im Plenum besprechen, aber eine Musterlösung bereit stellen.